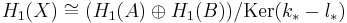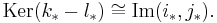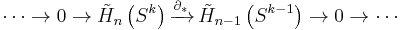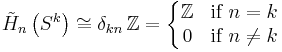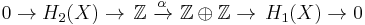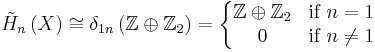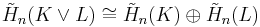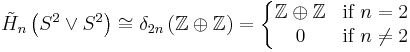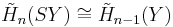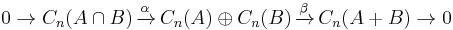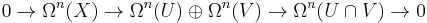Mayer–Vietoris sequence
In mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces, known as their homology and cohomology groups. The result is due to two Austrian mathematicians, Walther Mayer and Leopold Vietoris. The method consists of splitting a space into pieces, called subspaces, for which the homology or cohomology groups may be easier to compute. The sequence relates the (co)homology groups of the space to the (co)homology groups of the subspaces. It is a natural long exact sequence, whose entries are the (co)homology groups of the whole space, the direct sum of the (co)homology groups of the subspaces, and the (co)homology groups of the intersection of the subspaces.
The Mayer–Vietoris sequence holds for a variety of cohomology and homology theories, including singular homology and singular cohomology. In general, the sequence holds for those theories satisfying the Eilenberg-Steenrod axioms, and it has variations for both reduced and relative (co)homology. Because the (co)homology of most spaces cannot be computed directly from their definitions, one uses tools such as the Mayer–Vietoris sequence in the hope of obtaining partial information. Many spaces encountered in topology are constructed by piecing together very simple patches. Carefully choosing the two covering subspaces so that, together with their intersection, they have simpler (co)homology than that of the whole space may allow a complete deduction of the (co)homology of the space. In that respect, the Mayer–Vietoris sequence is analogous to the Seifert–van Kampen theorem for the fundamental group, and a precise relation exists for homology of dimension one.
Contents |
Background, motivation, and history
Like the fundamental group or the higher homotopy groups of a space, homology groups are important topological invariants. Although some (co)homology theories are computable using tools of linear algebra, many other important (co)homology theories, especially singular (co)homology, are not computable directly from their definition for nontrivial spaces. For singular (co)homology, the singular (co)chains and (co)cycles groups are often too big to handle directly. More subtle and indirect approaches become necessary. The Mayer–Vietoris sequence is such an approach, giving partial information about the (co)homology groups of any space by relating it to the (co)homology groups of two of its subspaces and their intersection.
The most natural and convenient way to express the relation involves the algebraic concept of exact sequences: sequences of objects (in this case groups) and morphisms (in this case group homomorphisms) between them such that the image of one morphism equals the kernel of the next. In general, this does not allow (co)homology groups of a space to be completely computed. However, because many important spaces encountered in topology are topological manifolds, simplicial complexes, or CW complexes, which are constructed by piecing together very simple patches, a theorem such as that of Mayer and Vietoris is potentially of broad and deep applicability.
Mayer was introduced to topology by his colleague Vietoris when attending his lectures in 1926 and 1927 at a local university in Vienna.[1] He was told about the conjectured result and a way to its solution, and solved the question for the Betti numbers in 1929.[2] He applied his results to the torus considered as the union of two cylinders.[3][4] Vietoris later proved the full result for the homology groups in 1930 but did not express it as an exact sequence.[5] The concept of an exact sequence only appeared in print in the 1952 book Foundations of Algebraic Topology by Samuel Eilenberg and Norman Steenrod[6] where the results of Mayer and Vietoris were expressed in the modern form.[7]
Basic versions for singular homology
Let X be a topological space and A, B be two subspaces whose interiors cover X. (The interiors of A and B need not be disjoint.) The Mayer–Vietoris sequence in singular homology for the triad (X, A, B) is a long exact sequence relating the singular homology groups (with coefficient group the integers Z) of the spaces X, A, B, and the intersection A∩B.[8] There is an unreduced and a reduced version.
Unreduced version
For unreduced homology, the Mayer–Vietoris sequence states that the following sequence is exact:[9]
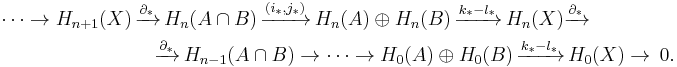
Here the maps i : A∩B ↪ A, j : A∩B ↪ B, k : A ↪ X, and l : B ↪ X are inclusion maps and  denotes the direct sum of abelian groups.
denotes the direct sum of abelian groups.
Boundary map
The boundary maps ∂* lowering the dimension may be made explicit as follows.[10] An element in Hn(X) is the homology class of an n-cycle x which, by barycentric subdivision for example, can be written as the sum of two n-chains u and v whose images lie wholly in A and B, respectively. Thus ∂x = ∂(u + v) = 0 so that ∂u = −∂v. This implies that the images of both these boundary (n − 1)-cycles are contained in the intersection A∩B. Then ∂*([x]) is the class of ∂u in Hn−1(A∩B). Choosing a different representative x′ does not affect ∂u since ∂x′ = ∂x = 0; nor does choosing another decomposition x = u′ + v′ since then ∂u + ∂v − ∂u′ − ∂v′ = 0 which implies ∂u = ∂u′ and ∂v = ∂v′. Notice that the maps in the Mayer–Vietoris sequence depend on choosing an order for A and B. In particular, the boundary map changes sign if A and B are swapped.
Reduced version
For reduced homology there is also a Mayer–Vietoris sequence, under the assumption that A and B have non-empty intersection.[11] The sequence is identical for positive dimensions and ends as:
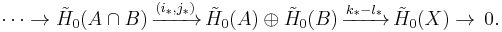
Analogy with the Seifert–van Kampen theorem
There is an analogy between the Mayer–Vietoris sequence (especially for homology groups of dimension 1) and the Seifert–van Kampen theorem.[10][12] Whenever A∩B is path-connected the reduced Mayer–Vietoris sequence yields the isomorphism
where, by exactness,
This is precisely the abelianized statement of the Seifert–van Kampen theorem. Compare with the fact that H1(X) is the abelianization of the fundamental group π1(X) when X is path-connected.[13]
Basic applications
k-sphere
To completely compute the homology of the k-sphere X = Sk, let A and B be two hemispheres of X with intersection homotopic to a (k − 1)-dimensional equatorial sphere. Since the k-dimensional hemispheres are homeomorphic to k-discs, which are contractible, the homology groups for A and B are trivial. The Mayer–Vietoris sequence for reduced homology groups then yields
Exactness immediately implies that the map ∂* is an isomorphism. Using the reduced homology of the 0-sphere (two points) as a base case, it follows[14]
where δ is the Kronecker delta. Such a complete understanding of the homology groups for spheres is in stark contrast with current knowledge of homotopy groups of spheres, especially for the case n > k about which little is known.[15]
Klein bottle
A slightly more difficult application of the Mayer–Vietoris sequence is the calculation of the homology groups of the Klein bottle X. One uses the decomposition of X as the union of two Möbius strips A and B glued along their boundary circle (see illustration on the right). Then A, B and their intersection A∩B are homotopy equivalent to circles, so the nontrivial part of the sequence yields[16]
and the trivial part implies vanishing homology for dimensions greater than 2. The central map α sends 1 to (2, −2) since the boundary circle of a Möbius band wraps twice around the core circle. In particular α is injective so homology of dimension 2 also vanishes. Finally, choosing (1, 0) and (1, −1) as a basis for Z2, it follows
Wedge sums
Let X be the wedge sum of two spaces K and L, and suppose furthermore that the identified basepoint is a deformation retract of open neighborhoods U ⊂ K and V ⊂ L. Letting A = K∪V and B = U∪L it follows that A∪B = X and A∩B = U∪V, which is contractible by construction. The reduced version of the sequence then yields (by exactness)[17]
for all dimensions n. The illustration on the right shows X as the sum of two 2-spheres K and L. For this specific case, using the result from above for 2-spheres, one has
Suspensions
If X is the suspension SY of a space Y, let A and B be the complements in X of the top and bottom 'vertices' of the double cone, respectively. Then X is the union A∪B, with A and B contractible. Also, the intersection A∩B is homotopy equivalent to Y. Hence the Mayer–Vietoris sequence yields, for all n,[18]
The illustration on the right shows the 1-sphere X as the suspension of the 0-sphere Y. Noting in general that the k-sphere is the suspension of the (k − 1)-sphere, it is easy to derive the homology groups of the k-sphere by induction, as above.
Further discussion
Relative form
A relative form of the Mayer–Vietoris sequence also exists. If Y ⊂ X and is the union of C ⊂ A and D ⊂ B, then the exact sequence is:[19]
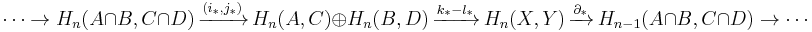
Naturality
The homology groups are natural in the sense that if ƒ is a continuous map from X1 to X2, then there is a canonical pushforward map ƒ∗ of homology groups ƒ∗ : Hk(X1) → Hk(X2), such that the composition of pushforwards is the pushforward of a composition: that is, 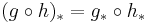 . The Mayer–Vietoris sequence is also natural in the sense that if X1 = A1∪B1 to X2 = A2∪B2 and the mapping ƒ satisfies ƒ(A1) ⊂ A2 and ƒ(B1) ⊂ B2, then the connecting morphism ∂∗ of the Mayer–Vietoris sequence commutes with ƒ∗.[20] That is,[21] the following diagram commutes (the horizontal maps are the usual ones):
. The Mayer–Vietoris sequence is also natural in the sense that if X1 = A1∪B1 to X2 = A2∪B2 and the mapping ƒ satisfies ƒ(A1) ⊂ A2 and ƒ(B1) ⊂ B2, then the connecting morphism ∂∗ of the Mayer–Vietoris sequence commutes with ƒ∗.[20] That is,[21] the following diagram commutes (the horizontal maps are the usual ones):
Cohomological versions
The Mayer–Vietoris long exact sequence for singular cohomology groups with coefficient group G is dual to the homological version. It is the following:[22]
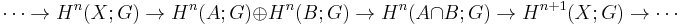
where the dimension preserving maps are restriction maps induced from inclusions, and the (co-)boundary maps are defined in a similar fashion to the homological version. There is also a relative formulation.
As an important special case when G is the group of real numbers R and the underlying topological space has the additional structure of a smooth manifold, the Mayer–Vietoris sequence for de Rham cohomology is
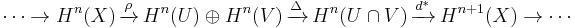
where {U, V} is an open cover of X, ρ denotes the restriction map, and Δ is the difference. The map d* is defined similarly as the map ∂* from above. It can be briefly described as follows. For a cohomology class [ω] represented by closed form ω in U∩V, express ω as a difference of forms ωU - ωV via a partition of unity subordinate to the open cover {U, V}, for example. The exterior derivative dωU and dωV agree on U∩V and therefore together define an n + 1 form σ on X. One then has d*([ω]) = [σ].
Derivation
Consider the long exact sequence associated to the short exact sequences of chain groups (constituent groups of chain complexes)
where α(x) = (x, −x), β(x, y) = x + y, and Cn(A + B) is the chain group consisting of sums of chains in A and chains in B.[9] It is a fact that the singular n-simplices of X whose images are contained in either A or B generate all of the homology group Hn(X).[23] In other words, Hn(A + B) is isomorphic to Hn(X). This gives the Mayer–Vietoris sequence for singular homology.
The same computation applied to the short exact sequences of vector spaces of differential forms
yields the Mayer–Vietoris sequence for de Rham cohomology.[24]
From a formal point of view, the Mayer–Vietoris sequence can be derived from the Eilenberg–Steenrod axioms for homology theories using the long exact sequence in homology.[25]
Other homology theories
The derivation of the Mayer–Vietoris sequence from the Eilenberg–Steenrod axioms does not require the dimension axiom,[26] so in addition to existing in ordinary cohomology theories, it holds in extraordinary cohomology theories (such as topological K-theory and cobordism).
Sheaf cohomology
From the point of view of sheaf cohomology, the Mayer–Vietoris sequence is related to Čech cohomology. Specifically, it arises from the degeneration of the spectral sequence that relates Čech cohomology to sheaf cohomology (sometimes called the Mayer–Vietoris spectral sequence) in the case where the open cover used to compute the Čech cohomology consists of two open sets.[27] This spectral sequence exists in arbitrary topoi.[28]
See also
Notes
- ^ Hirzebruch 1999
- ^ Mayer 1929
- ^ Dieudonné 1989, p. 39
- ^ Mayer 1929, p. 41
- ^ Vietoris 1930
- ^ Corry 2004, p. 345
- ^ Eilenberg & Steenrod 1952, Theorem 15.3
- ^ Eilenberg & Steenrod 1952, §15
- ^ a b Hatcher 2002, p. 149
- ^ a b Hatcher 2002, p. 150
- ^ Spanier 1966, p. 187
- ^ Massey 1984, p. 240
- ^ Hatcher 2002, Theorem 2A.1, p. 166
- ^ Hatcher 2002, Example 2.46, p. 150
- ^ Hatcher 2002, p. 384
- ^ Hatcher 2002, p. 151
- ^ Hatcher 2002, Exercise 31
- ^ Hatcher 2002, Exercice 32
- ^ Hatcher 2002, p. 152
- ^ Massey 1984, p. 208
- ^ Eilenberg & Steenrod 1952, Theorem 15.4
- ^ Hatcher 2002, p. 203
- ^ Hatcher 2002, Proposition 2.21, p. 119
- ^ Bott & Tu 1982, §I.2
- ^ Hatcher 2002, p. 162
- ^ Kōno & Tamaki 2006, pp. 25–26
- ^ Dimca 2004, pp. 35–36
- ^ Verdier 1972 (SGA 4.V.3)
References
- Bott, Raoul; Tu, Loring W. (1982), Differential Forms in Algebraic Topology, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90613-3.
- Corry, Leo (2004), Modern Algebra and the Rise of Mathematical Structures, Birkhäuser, p. 345, ISBN 3764370025.
- Dieudonné, Jean (1989), A History of Algebraic and Differential Topology 1900-1960, Birkhäuser, p. 39, ISBN 081763388X.
- Dimca, Alexandru (2004), Sheaves in topology, Universitext, Berlin: Springer-Verlag, ISBN 978-3-540-20665-1, MR2050072
- Eilenberg, Samuel; Steenrod, Norman (1952), Foundations of Algebraic Topology, Princeton University Press, ISBN 978-0691079653.
- Hatcher, Allen (2002), Algebraic Topology, Cambridge University Press, ISBN 978-0-521-79540-1, MR1867354, http://www.math.cornell.edu/%7Ehatcher/AT/ATpage.html.
- Hirzebruch, Friedrich (1999), "Emmy Noether and Topology", in Teicher, M., The Heritage of Emmy Noether, Israel Mathematical Conference Proceedings, Bar-Ilan University/American Mathematical Society/Oxford University Press, pp. 61–63, ISBN 978-0198510451, OCLC 223099225.
- Kōno, Akira; Tamaki, Dai (2006) [2002], Generalized cohomology, Iwanami Series in Modern Mathematics, Translations of Mathematical Monographs, 230 (Translated from the 2002 Japanese edition by Tamaki ed.), Providence, RI: American Mathematical Society, ISBN 978-0-821-83514-2, MR2225848
- Massey, William (1984), Algebraic Topology: An Introduction, Springer-Verlag, ISBN 9780387902715.
- Mayer, Walther (1929), "Über abstrakte Topologie", Monatshefte für Mathematik 36 (1): 1–42, doi:10.1007/BF02307601, ISSN 0026-9255, http://www.springerlink.com/content/x33611021p942518/. (German)
- Spanier, Edwin (1966), Algebraic Topology, Springer-Verlag, ISBN 0-387-94426-5.
- Verdier, Jean-Louis (1972), "Cohomologie dans les topos", in Artin, Michael; Grothendieck, Alexander; Verdier, Jean-Louis (in French), Séminaire de Géométrie Algébrique du Bois Marie - 1963–64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - Tome 2, Lecture Notes in Mathematics, 270, Berlin; Heidelberg: Springer-Verlag, pp. 1, doi:10.1007/BFb0061320, ISBN 978-3-540-06012-3
- Vietoris, Leopold (1930), "Über die Homologiegruppen der Vereinigung zweier Komplexe", Monatshefte für Mathematik 37: 159–62, doi:10.1007/BF01696765. (German)
Further reading
- Reitberger, Heinrich (2002), "Leopold Vietoris (1891–2002)" (PDF), Notices of the American Mathematical Society 49 (20), ISSN 0002-9920, http://www.ams.org/notices/200210/fea-vietoris.pdf.